Introduction

Most of the times in graphics we do come across case when we are given some vectors and, we want to define co-ordinate system.

For example, If we want our camera to follow the character in the scene and, we have position of camera and position of the character.

Now in order to do this we will need to find co-ordinate system for camera.

In other words, we need to find orthonormal basis.

Othnormal basis is nothing but set of vectors perpendicular to each other and unit in length.

Given orthonormal basis by using linear combinations of the vectors defining basis, we can derive any vector in the given space.

In our case we can treat co-ordinate system of camera as vector space of 3D vectors.

Algorithm

For this purpose we can use process called as Grahm schmidt which is as follows

In order to find orthonormal basis for camera we have two vectors

• v - Vector got using position of character and position of camera.

  u - Vector got using position of camera and origin of world co-ordinate system.

  Note : Camera is placed in scene with respect to some world co-ordinate system.

• Select vector v and normalize it.

  Note : We want out final vectors in orthonormal basis to be unit vectors.

  Select vector u and find projection of u onto v.

  Please see below for formula :

  

  For us the projection is simplified to :  **(u.v) * v **

Please remembder projection of u onto v will give us new vector lets call it projvu which is in the direction of v.

• Now using following equation we get new vector which is perpendicular to v and projvu . Lets call it s.

  Please see image below :

  

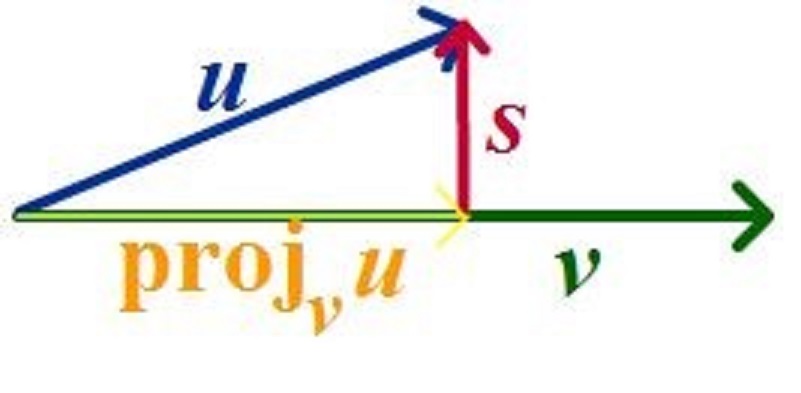
   s = u - projvu ; 
   s = normalize(s);

• Now we have v and s which are unit vectors and perpendicular to each other.

  We just need one more unit and perpendicular vector to complete the orthonormal basis.

  We can achieve it using following formula.

   t = normalize(v X s)

Hence starting with a vector we got orthonormal basis defined by vectors v,s,t for camera.

Extending to n-Dimension

I have shown above method for set of 3 dimensional vectors.This process can easily be extended to n dimensional set of vectors.

Here set of vector u(1……k) are orthogonal and vector e(1……k) forms orthonormal basis.